
In part 2, I used htm.core as a single order sequence memory by allowing only one cell per mini-column. In this post I’ll finally have a first look at the high order sequence memory.
Before we do that, I want to show you one last single order memory example however.
Single Order Sequence Memory Recap
As you might remember from the last post, these were the settings for our htm.core temporal memory (aka sequence memory).
columns = 8
inputSDR = SDR( columns )
cellsPerColumn = 1
tm = TM(columnDimensions = (inputSDR.size,),
cellsPerColumn = cellsPerColumn, # default: 32
minThreshold = 1, # default: 10
activationThreshold = 1, # default: 13
initialPermanence = 0.4, # default: 0.21
connectedPermanence = 0.5, # default: 0.5
permanenceIncrement = 0.1, # default: 0.1
permanenceDecrement = 0.1, # default: 0.1
predictedSegmentDecrement = 0.0, # default: 0.0
maxSegmentsPerCell = 1, # default: 255
maxSynapsesPerSegment = 1 # default: 255
)
We have seen that the TM doesn’t really have a chance to learn the following sequence of ascending and descending numbers successfully.
cycleArray = [0, 1, 2, 3, 4, 5, 6, 7, 6, 5, 4, 3, 2, 1]
You might wonder, if changing the maxSegementPerCell and maxSynapsesPerSegement actually makes any difference. Therefore, let’s just test this out, using the console application again.
At cycle 2, step 8 the connections for the increasing numbers part of the sequence have reached a permanence of 0.5 and therefore are considered as connected.
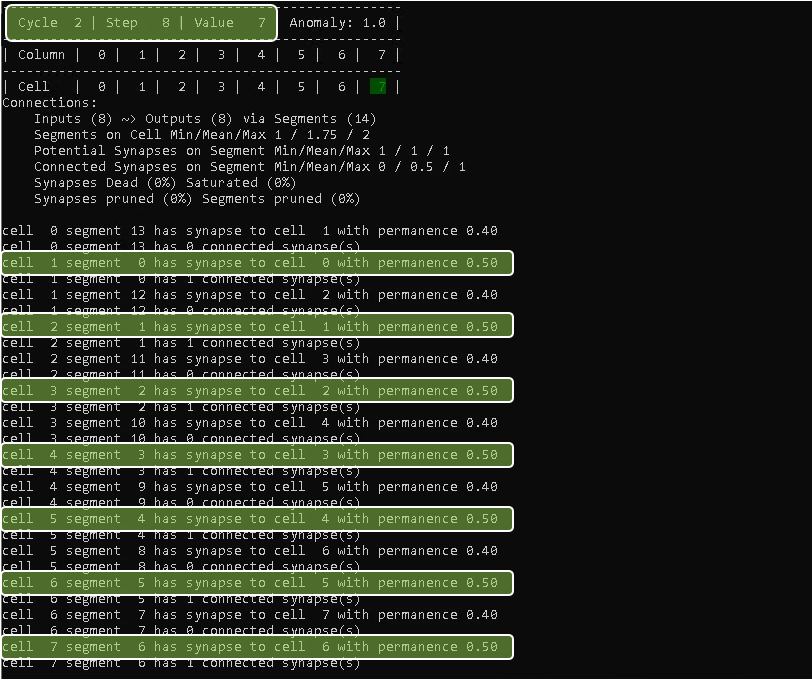
Once cycle 3, step 1 is reached, the synapses for the descending values are considered as connected as well.
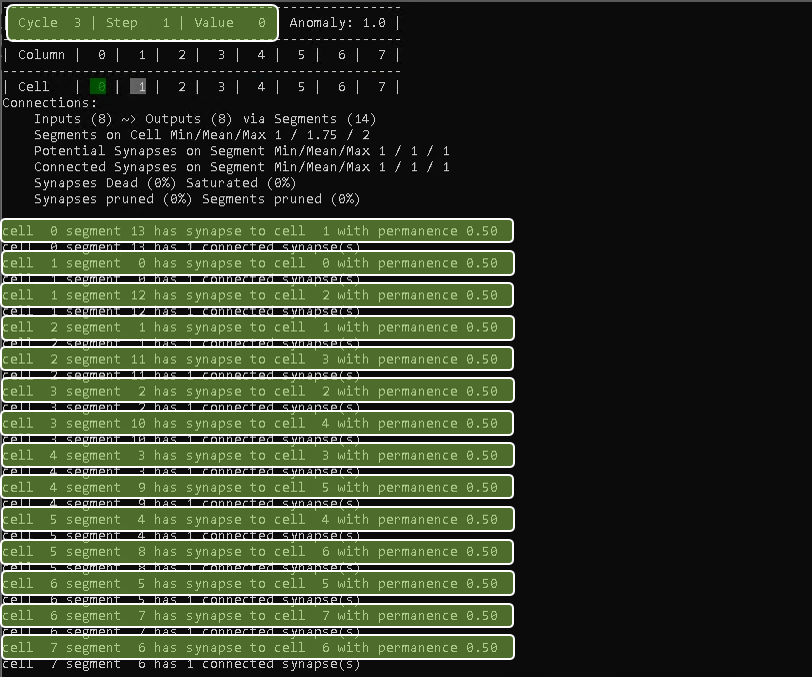
Looking at cycle 3, step 2 for example, you will notice that the TM now predicts its two neighbor cells as potential winner cells for the next step, as it has seen both values (0 and 2) coming up next in the sequence at a certain point in time.
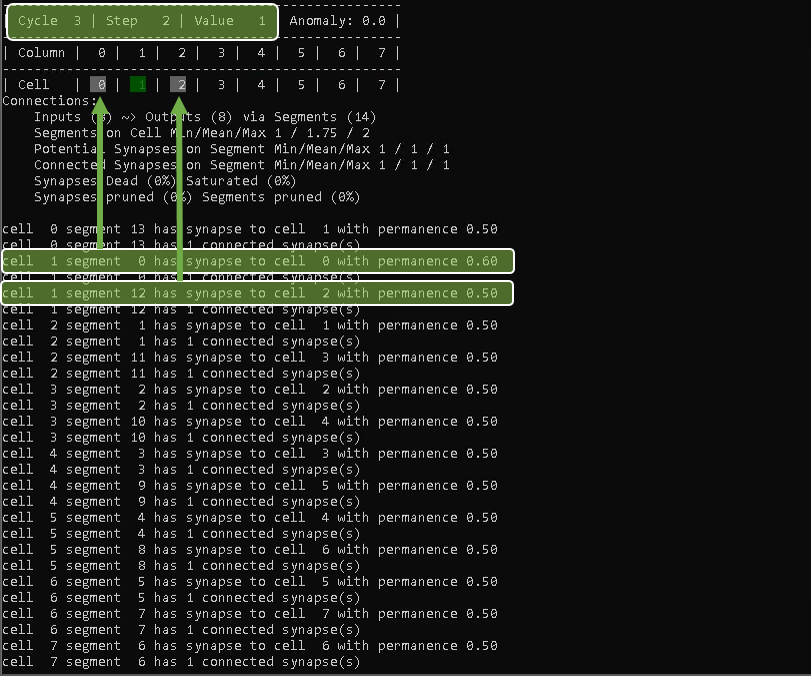
Cells 0 and 7 obviously don’t have this issue, since the only value coming after 0 is 1, and the only value after 7 is 6.
Aright. It’s finally time to say goodbye to the single order memory, which is just using one cell per column, and welcome the…
High Order Sequence Memory
Besides setting the htm.core TM parameter cellsPerColumn to 2, I also set maxSegmentsPerCell and maxSynapsesPerSegment back to 1.
columns = 8
inputSDR = SDR( columns )
cellsPerColumn = 2
tm = TM(columnDimensions = (inputSDR.size,),
cellsPerColumn = cellsPerColumn, # default: 32
minThreshold = 1, # default: 10
activationThreshold = 1, # default: 13
initialPermanence = 0.4, # default: 0.21
connectedPermanence = 0.5, # default: 0.5
permanenceIncrement = 0.1, # default: 0.1
permanenceDecrement = 0.1, # default: 0.1
predictedSegmentDecrement = 0.0, # default: 0.0
maxSegmentsPerCell = 1, # default: 255
maxSynapsesPerSegment = 1 # default: 255
)
BTW: If you are used to experiment with the Numenta NuPIC library and want to switch to htm.core, here is a very useful mapping chart of the different parameters.
Time to see it in action now.
Hurray!
When the sequence memory sees the value 6 the second time now (coming from 7), it knows that this is in a different context than for the first time (coming from value 5). But this time it can, and does, use the second cell of the column to memorize that context. It simply could not do this as a single order temporal memory.
You probably also noticed that cell 1 and 15 (the second cells in column 0 and 7) are not used. Again, this is because there is only ever one context in which the numbers 0 and 7 are seen.
“What happens, if I use more than 2 cells per column?” you might ask?
Well, since each value in the sequence is only seen in a maximum of two different contexts, using more cells per column wouldn’t make a difference.
Just try it out yourself. For example, by using the code at the end of “htm.core parameters – Single Order Sequence Memory“
Houston, we …?
The sequence used so far was very simple and defined like this:
cycleArray = [0, 1, 2, 3, 4, 5, 6, 7, 6, 5, 4, 3, 2, 1]
Let’s make it a bit more interesting by looking at the following sequence:
cycleArray = [0, 1, 2, 2, 3, 4, 5, 5, 6, 7, 6, 5, 4, 3, 3, 2, 2, 1]
Visualizing this new sequence along with its different connections doesn’t work that well with the previously used console application. Therefore, I’ve imported the htm.core library into Blender and used it to script the animation below.
Let’s have a closer look at what’s going on here.
The first step
In the first step we can see that all cells of the first column are activated (blue) and one of them is picked by the TM algorithm as a winner cell (green). The reason why all the cells within a column are activated is, that there are no connections greater than, or equal to the connectedPermanence threshold yet.
This mechanism of activating all cells initially is called bursting and will continue until one of the cells in a column enters a predictive state. Meaning that it is considered connected.
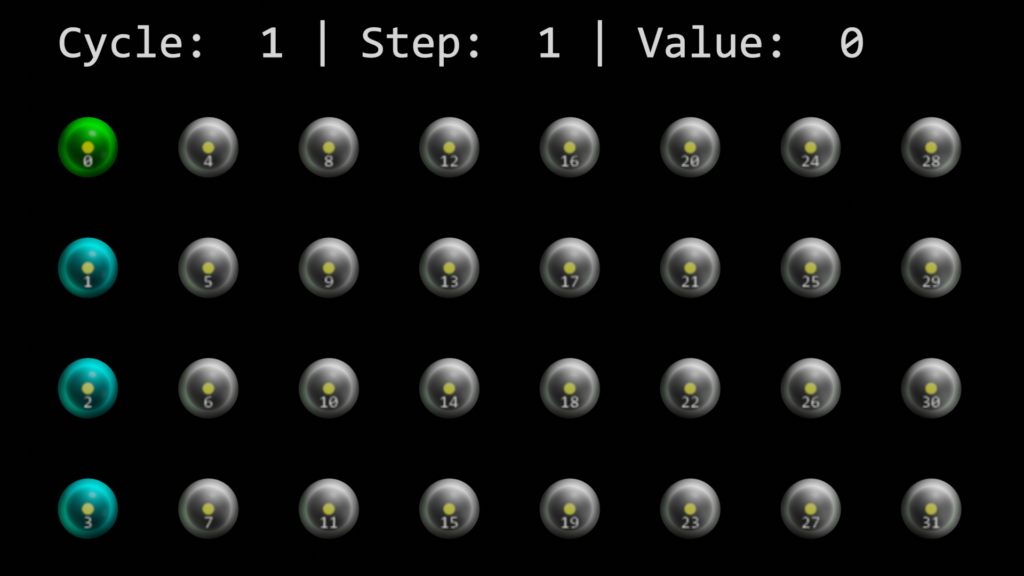
Winner cells
Whenever a column is activated and the value is seen in a new context, a new cell in the column is picked, if available. That’s why the 3rd cell in the column for value 5 is the winner cell in the screenshot below. The first time it saw value 5 in the context of value 4, then with value 5 and the 3rd time coming from value 6.
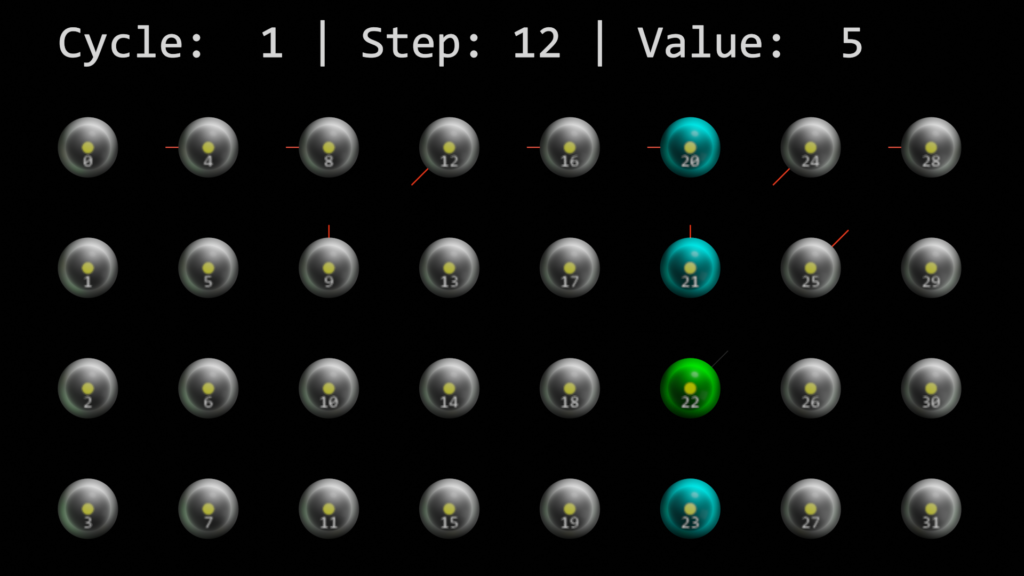
Connections
You can also see how the connections to the other cells start to build out. Red means that they are not considered as connected (< connectedPermanence). They will turn green, once connected, however.
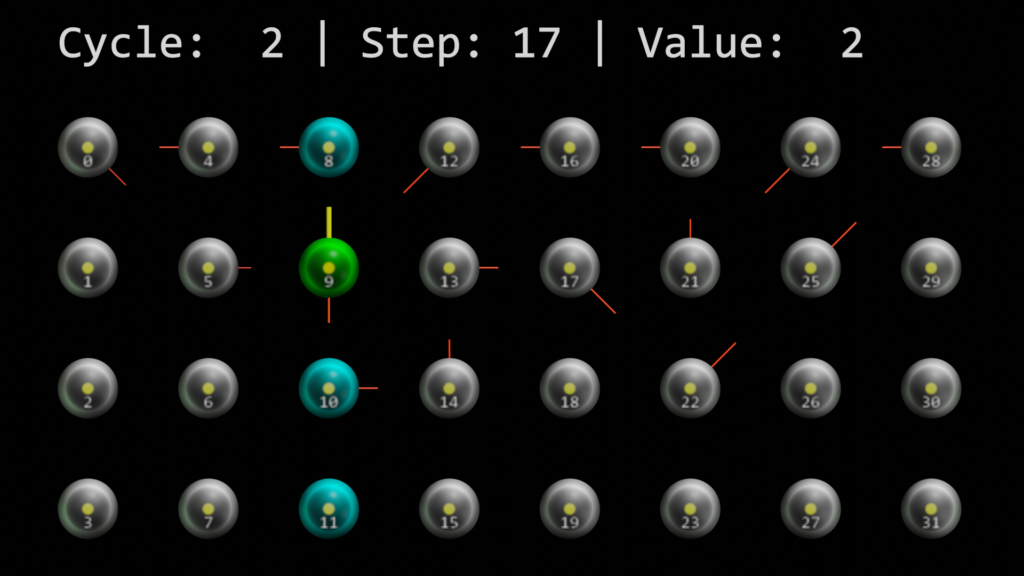
Watching the video you might have noticed that the second cell within the column that represents the value 2 (cell 9), does reach the connectedPermanence threshold much faster than the other cells. Well, here’s our sequence again.
cycleArray = [0, 1, 2, 2, 3, 4, 5, 5, 6, 7, 6, 5, 4, 3, 3, 2, 2, 1]
As you can see, step 4 and step 17 are both seeing number 2 in the same context, which actually is the number 2 itself.
Order matters
It’s worth to mention, that in htm.core the computation of the active/winner cell(s) and the dendrites (connections) are split into two steps.
tm.compute(inputSDR, learn = True) tm.activateDendrites(True)
And predictive cells can be calculated after the dendrites are activated, only.
predictedCells = tm.getPredictiveCells()
Predicted cell
Cycle 3, step 3 is the first time we see a predicted cell. In the visualization a predicted cell is colored yellow. In the screenshot below, cell 9 is not only predicted, but an active cell as well. And, since the winner cell 8 of that column is not connected yet, the whole column bursts.
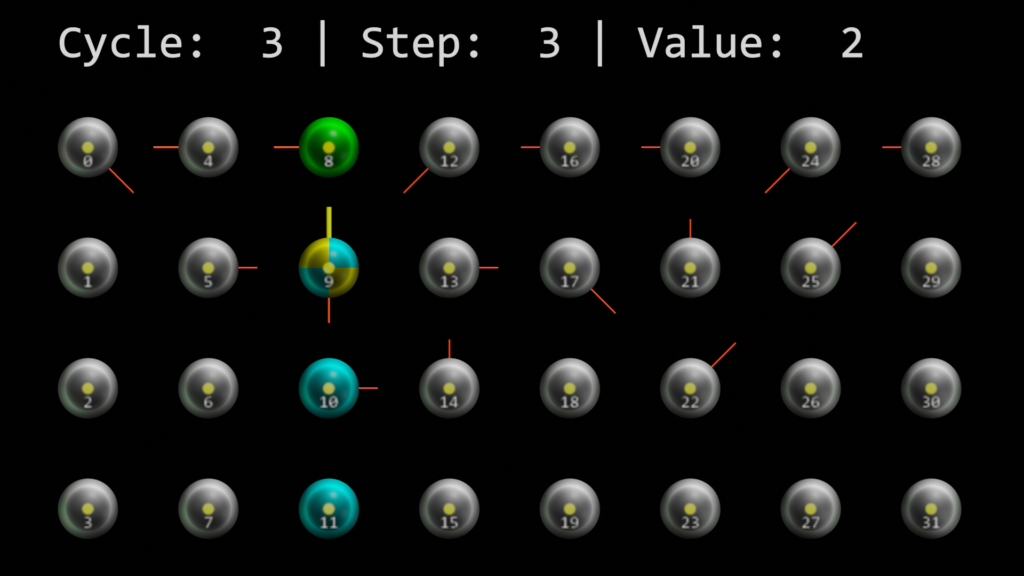
Cell 9 builds connections to cell 8 (the cell that sees the value 2 in the context of value 1) and cell 10 (the one that sees value 2 coming from value 3 in the sequence).
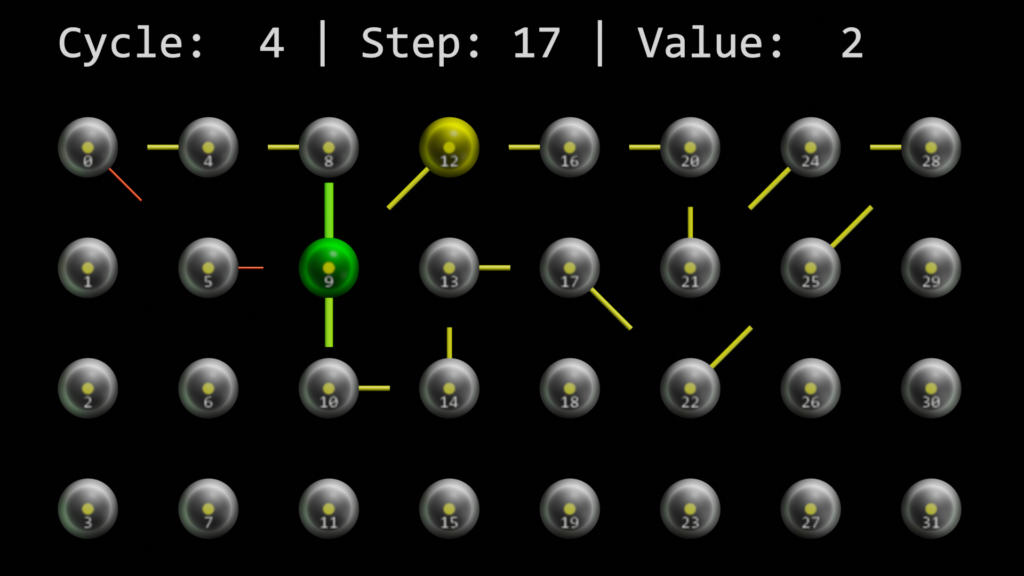
And cell 9 continues to be interesting. Cycle 5, step 4 shows, that either the number 1, or the number 3 are predicted after our sequence of 2 twos. This is correct, but – as with the single order memory – it can’t really decide which one is correct, as it always just looks at the difference of one time step.
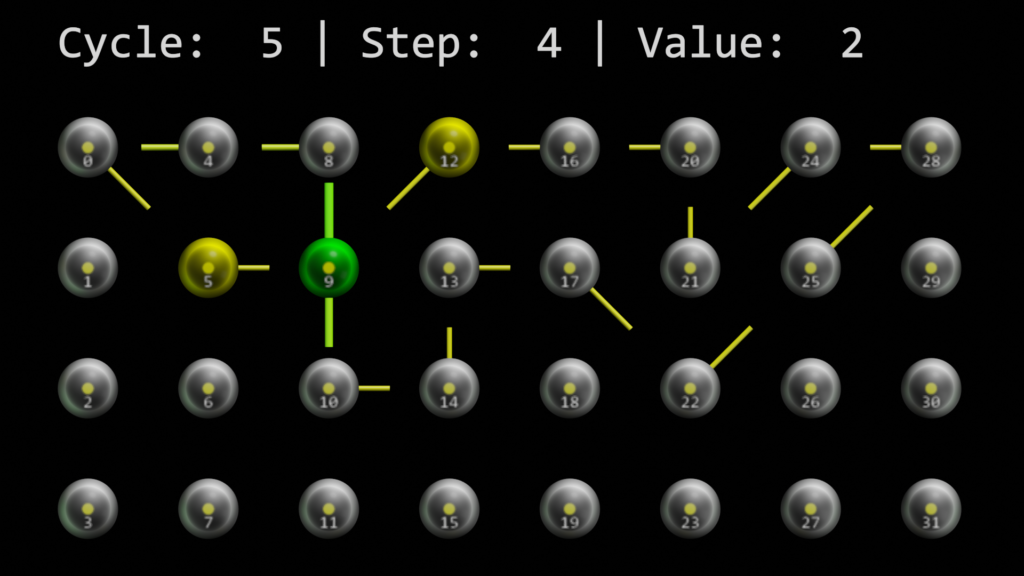
This is actually a known behavior of the algorithm. Below are some links to related discussions at the Numenta forum:
- https://discourse.numenta.org/t/exploring-the-repeating-inputs-problem/5498
- https://discourse.numenta.org/t/htm-is-so-much-more-than-show-tunes/3639
- https://discourse.numenta.org/t/my-analysis-on-why-temporal-memory-prediction-doesnt-work-on-sequential-data/3141
What’s next?
You may now wonder what impact the behavior discovered above might have. Don’t worry. There’s actually much more to HTM than just the temporal memory. The Spatial Pooler and encoders play an important part in the overall picture as well. That’s why I’ll start to have a closer look into them in one of the next posts.
I know that there are still some parameters of the htm.core Temporal Memory that I haven’t covered yet. AnomalyMode probably being the most interesting one. I will have a closer look at it, once I show how the combination of Encoder, Spatial Pooler and Temporal Memory work together.
Last, but not least, I encourage you to watch the following HTM School videos again.
